Class 10 Maths Important Formulas for Last Minute Revision for Board Exam 2023

CBSE Class 10 Maths Board Exam 2023 Important Formulas: Check here all the important formulas from all chapters of CBSE Class 10 Maths for quick revision checklist. Make sure to check all Important terms and properties useful for the upcoming Class 10 Maths board exam calculations on March 21, 2023.

Important Formulas for CBSE 10th Maths Exam 2023: Maths is a subject feared irrationally by students, in general. Although it can get a little tricky, it is not a subject where high scores are impossible. All you need to do is regular hard work and smart work. To help you have a good hold on all chapters of the CBSE Class 10 Maths curriculum, we have compiled here the important formulas for you to score high marks in the Maths exam. 

1. Real Numbers:

Euclid’s Division Algorithm (lemma): According to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r  such that a = bq + r, where 0 ≤ r ≤ b. (Here, a = dividend, b = divisor, q = quotient and r = remainder.)

2. Polynomials:

(i) (a + b)2 = a2 + 2ab + b2

(ii) (a – b)2  = a2 – 2ab + b2

(iii) a2 – b2 = (a + b) (a – b)

(iv) (a + b)3  = a3 + b3 + 3ab(a + b)

(v) (a – b)3  =  a3 – b3 – 3ab(a – b)

(vi) a3 + b3 = (a + b) (a2 – ab + b2)

(vii) a3 – b3  = (a – b) (a2 + ab + b2)

(viii) a4 – b4 = (a2)2 – (b2)2 = (a2 + b2) (a2 – b2) = (a2 + b2) (a + b) (a – b)

(ix) (a + b + c) 2  = a2 + b2 + c2 + 2ab + 2bc + 2ac

(x) (a + b – c) 2  =  a2 + b2 + c2 + 2ab – 2bc – 2ca

(xi) (a – b + c)2  = a2 + b2 + c2 – 2ab – 2bc + 2ca

(xii) (a – b – c)2  = a2 + b2 + c2 – 2ab +  2bc – 2ca

(xiii) a3 + b3 + c3 – 3abc  = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)

3. Linear Equations in Two Variables:

For the pair of linear equations

a1 + b1y + c1 = 0  and  a2 + b2y + c2 = 0,

the nature of roots (zeroes) or solutions is determined as follows:

(i) If a1/a2 ≠ b1/b2 then we get a unique solution and the pair of linear equations in two variables are consistent. Here, the graph consists of two intersecting lines.

(i) If a1/a2 ≠ b1/b2 ≠ c1/c2, then there exists no solution and the pair of linear equations in two variables are said to be inconsistent. Here, the graph consists of parallel lines.

(iii) If a1/a2 = b1/b2 = c1/c2, then there exists infinitely many solutions and the pair of lines are coincident and therefore, dependent and consistent. Here, the graph consists of coincident lines.

4. Quadratic Equation: 

For a quadratic equation, ax2 + bx + c = 0

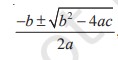
• Sum of roots = –b/a
• Product of roots = c/a
• If roots of a quadratic equation are given, then the quadratic equation can be represented as:

      x2 – (sum of the roots)x + product of the roots = 0

• If Discriminant > 0, then the roots the quadratic equation are real and unequal/unique.
• If Discriminant = 0, then the roots the quadratic equation are real and equal.
• If Discriminant < 0, then the roots the quadratic equation are imaginary (not real).

• Important Formulas – Boats and Streams

5. Arithmetic Progression:

• nth Term of an Arithmetic Progression: For a given AP, where a is the first term, d is the common difference, n is the number of terms, its nth term (an) is given as an = a + (n−1)×d

• Sum of First n Terms of an Arithmetic Progression, Sn is given as:
• 

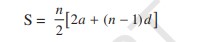
6. Similarity of Triangles:                                                                  

• If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
• Theorem on the area of similar triangles: If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.
• If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
• If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar
• If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
• The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
• If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other
• In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

7. Coordinate Geometry:

• Distance Formulae: Consider a line having two point A(x1, y1) and B(x2, y2), then the distance of these points is given as:
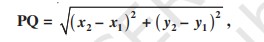
• Section Formula: If a point p divides a line AB with coordinates A(x1, y1) and B(x2, y2), in ratio m:n, then the coordinates of the point p are given as:
  
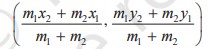
• Area of a Triangle: Consider the triangle formed by the points A(x1, y1) and B(x2, y2) and C(x3, y3) then the area of a triangle is given as-
  

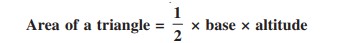
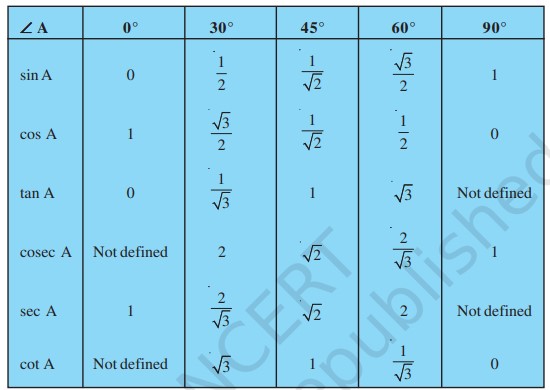
8. Trigonometry:

In a right-angled triangle, the Pythagoras theorem states

(perpendicular )2 + ( base )2 = ( hypotenuse )2

Important trigonometric properties:

(with P = perpendicular, B = base and H = hypotenuse)

• SinA = P / H
• CosA = B / H
• TanA = P / B
• CotA = B / P
• CosecA = H / P
• SecA = H/B

Trigonometric Identities:

• sin2A + cos2A=1
• tan2A +1 = sec2A
• cot2A + 1= cosec2A

Relations between trigonometric identities are given below:

Trigonometric Ratios of Complementary Angles are given as follows:

• sin (90° – A) = cos A
• cos (90° – A) = sin A
• tan (90° – A) = cot A
• cot (90° – A) = tan A
• sec (90° – A) = cosec A
• cosec (90° – A) = sec A

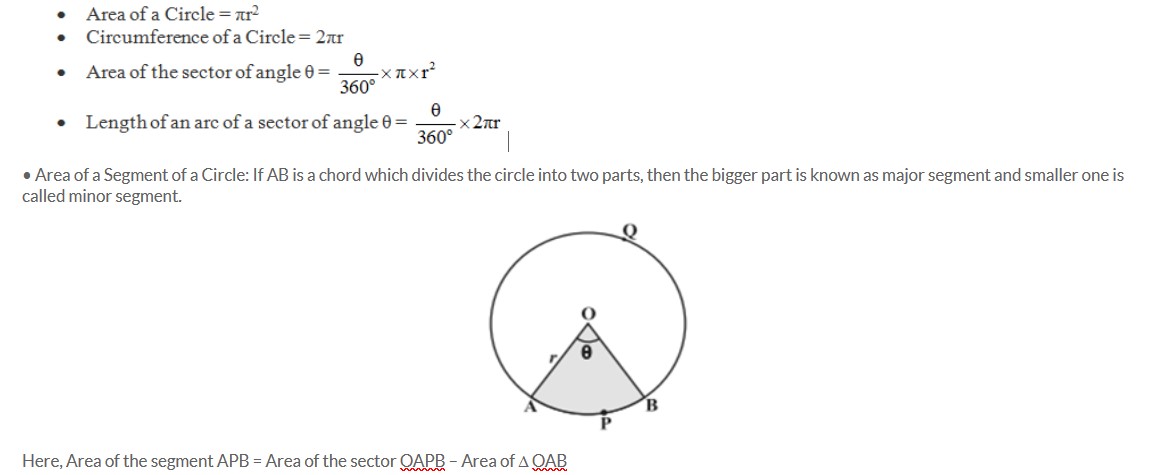
9. Circles:

Important properties related to circles:

• Equal chords of a circle are equidistant from the centre.
• The perpendicular drawn from the centre of a circle, bisects the chord of the circle.
• The angle subtended at the centre by an arc = Double the angle at any part of the circumference of the circle.
• Angles subtended by the same arc in the same segment are equal.
• To a circle, if a tangent is drawn and a chord is drawn from the point of contact, then the angle made between the chord and the tangent is equal to the angle made in the alternate segment.
• The sum of opposite angles of a cyclic quadrilateral is always 180o.

Important formulas related to circles:

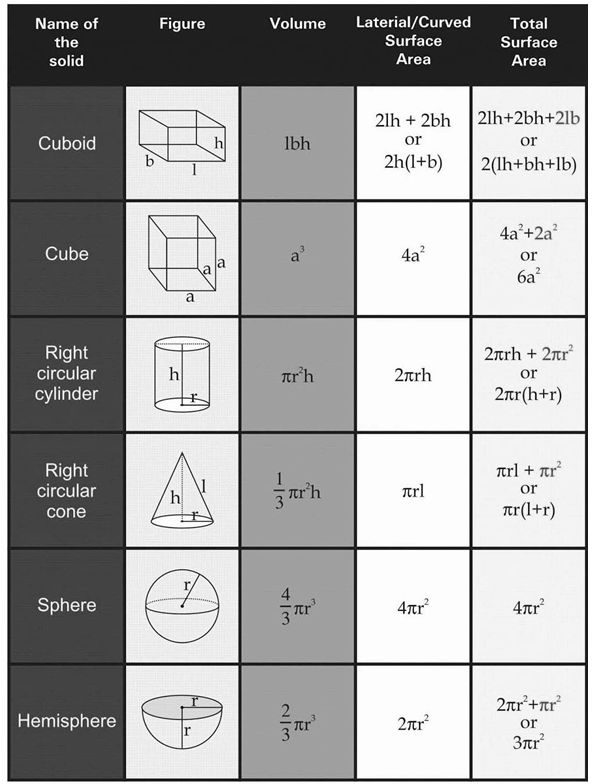
10. Mensuration:

Check below the important formulas for areas and volumes of solids:

11. Statistics

For Grouped Data:

Mean: If x1, x2, x3,……xn are observations with respective frequencies f1, f2, f3,…..fn then mean is given as:

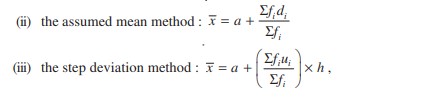
Median: For the given data, we need to have class interval, frequency distribution and cumulative frequency distribution. Then, median is calculated as

Where
l = lower limit of median class,
n = number of observations,
cf = cumulative frequency of class preceding the median class,
f = frequency of median class,
h = class size (assuming class size to be equal)

Mode: Modal class: The class interval having highest frequency is called the modal class and Mode is obtained using the modal class.

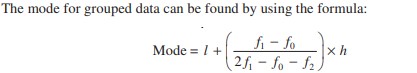
Where
l = lower limit of the modal class,
h = size of the class interval (assuming all class sizes to be equal),
f1 = frequency of the modal class,
f0 = frequency of the class preceding the modal class,
f2 = frequency of the class succeeding the modal class.

12. Probability:

Related resources: