Full Formula List for Classes 9, 10, 11 and 12th

Trigonometry Formulas: There are very few topics in mathematics that trouble students more than trigonometry and calculus. In fact, it is the base of many advanced math concepts and is also utilized in other subjects like physics. As such, it’s paramount that students learn trigonometry by heart. There are hundreds of formulas and identities that students have to memorize during their school time.

Trigonometry and subsequently calculus are a headache for students but necessary to clear the exams and pursue higher education in mathematics. Trigonometry also has many real-world applications.

As the name suggests, trigonometry is the branch of mathematics that deals with the study of the relationship between sides and angles of a right triangle. It’s used in astronomy, cartography, geography, naval and aviation industries. We bring you the following trigonometry formulas pdf.

Trigonometry Formulas PDF

Fundamentals of Trigonometry for Class 10

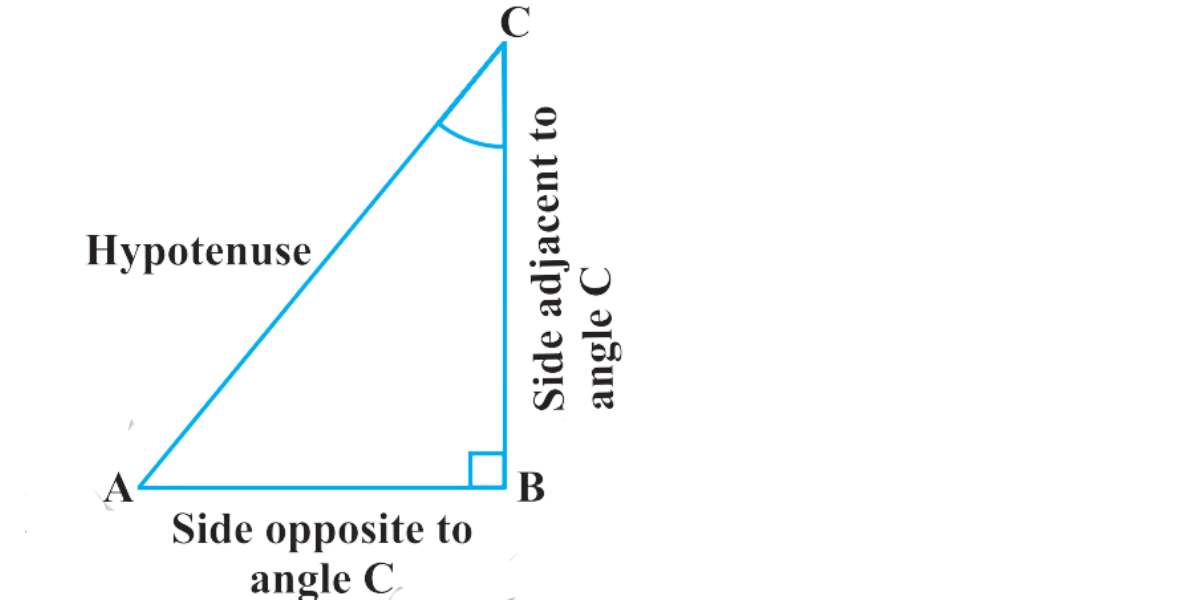
The trigonometric ratios of the angle A in right triangle ABC, given above are defined as follows:

• sine of ∠ A = side opposite to angle A/hypotenuse  = BC/AC
• cosine of ∠ A = side adjacent to angle A/hypotenuse = AB/AC
• tangent of ∠ A = side opposite to angle A/side adjacent to angle A = BC/AB
• cosecant of ∠ A = 1/sine of ∠A = AC/BC
• secant of ∠ A = 1/cosine of ∠A = AC/AB
• cotangent of ∠ A = 1/tangent of ∠A = AB/BC

Trigonometry Table

Trigonometric Co-Function Identities

• sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
• sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
• sin (3π/2 – A)  = – cos A & cos (3π/2 – A)  = – sin A
• sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
• sin (π – A) = sin A &  cos (π – A) = – cos A
• sin (π + A) = – sin A & cos (π + A) = – cos A
• sin (2π – A) = – sin A & cos (2π – A) = cos A
• sin (2π + A) = sin A & cos (2π + A) = cos A

Co-Function Identities In Degrees

• sin(90°−x) = cos x
• cos(90°−x) = sin x
• tan(90°−x) = cot x
• cot(90°−x) = tan x
• sec(90°−x) = cosec x
• cosec(90°−x) = sec x

Trigonometry Formulas for Class 12

Inverse Trigonometric Functions

READ: CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions Formulas List, Important Definitions & Examples

• sin^-1x = – sin^-1x
• cos^-1x = π – cos^-1x
• tan^-1(-x) = -tan^-1x
• cosec⁻¹(-x) = -cosec⁻¹x
• sec^-1(-x) = π – sec^-1x
• cot^-1(-x) = π – cot^-1x
• sin^-1x + cos^-1x = π/2
• tan^-1x + cot^-1x = π/2
• sec^-1x + cosec^-1x = π/2
• sin^-1x = – sin^-1x
• cos^-1x = π – cos^-1x
• tan^-1(-x) = -tan^-1x
• cosec⁻¹(-x) = -cosec⁻¹x
• sec^-1(-x) = π – sec^-1x
• cot^-1(-x) = π – cot^-1x
• sin^-1x + cos^-1x = π/2
• tan^-1x + cot^-1x = π/2
• sec^-1x + cosec^-1x = π/2

Double Of Inverse Trigonometric Functions

• 2tan^-1x = sin^-1(2x/1+ x²)
• = cos^-1(1-x²/1+x²)
• = tan^-1(2x/1-x²)
• 2sin^-1x = sin^-1(2x.√(1 – x²))
• 2cos^-1x = cos^-1(2x²– 1)

Triple Of Inverse Trigonometric Functions

• 3sin^-1x = sin^-1(3x – 4x³)
• 3cos^-1x = cos^-1(4x³– 3x)
• 3tan^-1x = tan^-1(3x – x³/1 – 3x²)