Maths Determinants Formulas: Determinants, along with matrices, is one of the most important topics in mathematics. The CBSE Class 11 and 12 introduce students to determinants, and the concept is also used in other subjects like physics, accountancy or computer science.
Determinants is a key chapter from an exam point of view as well. And since it’s closely linked with matrices, you have to know that chapter by heart before starting with determinants.
We have provided relevant source material for both the chapter here, along with the many formulas, properties and definitions determinants consist of. They help simplify complex problems and sometimes can solve questions in a fraction of the time taken to solve them traditionally.
Here at Jagran Josh, we cover the list of all important formulas, definitions, and glossary of Determinants, along with relevant examples. You can check the CBSE Class 12 Maths Chapter 4 Determinants Formulas below.
Recommended:
CBSE Class 12 Maths Mind Map for Chapter 4 Determinants
CBSE Class 12 Maths Chapter 4 Determinants MCQs
CBSE Class 12 Maths Chapter 4 Determinants Formulas and Theorems
We have listed all the important formulas, definitions and properties of CBSE Class 12 Determinants here.
Definition
A determinant is a numerical scalar value associated with a square matrix.
If A = [aij], then determinant = det(A) or |A|
Properties of Determinants:
- The value of a determinant remains unchanged if matrix rows and columns are interchanged.
- If any two rows or columns are interchanged, the sign of determinant changes.
- If any two rows or columns are same, then the value of determinant is Zero.
- If each element of a row or column is multiplied by a constant k, then the value of determinant also multiplied by k.
- The determinant of the product of matrices is equal to product of their respective determinants.
- If some or all the elements of a row or column are expressed as a sum or two or more terms then the determinant can be expressed as a sum of two or more determinants.
|A| = |AT|, where AT = transpose of A
If A = [aij ]3×3 , then |k.A|= k3.|A|
Determinant Expansion Formula:

Minors and Cofactors
- Minor of an element x in a matrix is the determinant obtained after deleting the row and column containing the element.
- Cofactor of a matrix is the result after multiplying the minor with (-1)i+j.
Adjoint
The transpose of a cofactor matrix of the square matrix (A) is called adjoint (Adj A) of a matrix.
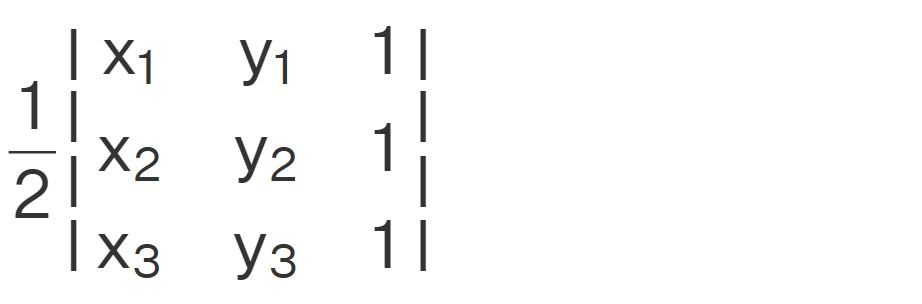
Area of Triangle
The area of a triangle on the Cartesian plane with the vertices (x1, y1), (x2, y2) (x3, y3) is given by
= (1/2) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Also Read
CBSE Class 12 Maths Syllabus 2023-24
CBSE Class 12 Maths Sample Paper 2023-24
NCERT Solutions for Class 12 Maths PDF
