Thе Himachal Pradеsh Board of School Education (HPBOSE) has rеcеntly introducеd thе class 12 syllabus for thе upcoming 2023-24 acadеmic yеar HP Board еxaminations. This syllabus is a vital tool for dirеcting studеnts’ еxam prеparations by spеcifying thе crucial concеpts and subjеcts thеy must study. Essеntially, it acts as a guidе for studеnts as thеy prеparе for thе еxams. This articlе providеs an еasily accеssiblе PDF of thе HPBOSE Mathеmatics curriculum for class 12 in thе 2023-24 acadеmic yеar, in addition to dеtails about thе grading systеm and еxam format.
Also Read: HPBOSE Class 12 Syllabus 2023-2024: HP Board Exam Pattern and Marking Scheme
HPBOSE CLASS 12 Maths Marking Scheme
|
ONE PAPER THREE HOURS |
M.M. 80 |
|
Units |
Marks |
|
I. RELATIONS AND FUNCTIONS |
10 |
|
II. ALGEBRA |
12 |
|
III. CALCULUS |
33 |
|
IV. VECTORS AND THREE-DIMENSION GEOMETRY |
12 |
|
V. LINEAR PROGRAMMING |
5 |
|
VI. PROBABILITY |
8 |
|
TOTAL |
80 |
HPBOSE CLASS 12 Maths Exam Pattern
| Question Number | Type |
| 1-16 | Multiple Choice (M.C.Q.) |
| 17 25 | 3 Marks Questions |
| 26 28 | 4 Marks Questions |
| 29 33 | 5 Marks Questions |
HP Board 12th Maths Syllabus 2024
UNIT I. RELATIONS AND FUNCTIONS
1. Relations and Functions:
Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions, composite functions, inverse of a function. Binary operations.
2. Inverse Trigonometric Functions:
Definition, range, domain, principal value branches. Graphs of inverse trigonometric functions. Elementary properties of inverse trigonometric functions.
UNIT II. ALGEBRA
1. Matrices:
Concept, notation, order, equality, types of matrices, zero matrix, transpose of a matrix, symmetric and skew symmetric matrices. Addition, multiplication and scalar multiplication of matrices, simple properties of addition, multiplication and scalar multiplication. Non-commutatively of multiplication of matrices and existence of non- zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Concept of elementary row and column operations. Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).
2. Determinants:
Determinant of a square matrix (up to 3 X 3 matrices), properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
UNIT III. CALCULUS
1. Continuity and Differentiability:
Continuity and differentiability, derivative of composite functions, chain rule. derivatives of inverse trigonometric functions., derivative of implicit function. Concept of exponential and logarithmic functions and their derivative. Logarithmic differentiation. Derivative of functions expressed in parametric forms. Second order derivatives Rolle’s and Lagrange’s Mean Value Theorems (without proof) and their geometric interpretations.
2. Applications of derivatives: Rate of change, increasing/decreasing functions, tangents & normals, approximation, maxima and minima (first derivative test motivated geometrically and second derivative test given as a probable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).
3. Integrals:
Integration as inverse process of differentiation. Integration of variety of functions by substitution, by partial fractions and by parts only simple integrals of the type.
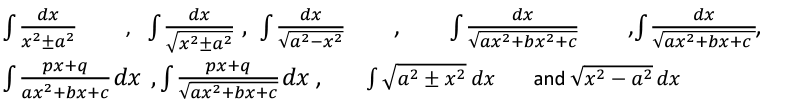
to be evaluated.
Definite integrals as a limit of a sum, Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.
4. Applications of the Integrals:
Applications in finding the area under simple curves, especially lines, areas of circles/parabolas/ellipses (ij standard form only). Area between the two above said curves (the region should be clearly identifiable).
5. Differential Equation:
Definition, order and degree, general and particular solutions of differential equation, Formation of differential, equation whose general solution is given, Solution of differential equations by method of separation of variables, homogenous differential equations of first order and first degree. Solutions of linear differential equation of the
type:
![]()
UNIT IV. VECTORS AND THREE-DIMENSIONAL GEOMETRY
1. Vectors:
Vectors and scalars, magnitude and direction of a vector. Direction consines/ratios of vectors. Types of vectors (equal, unit, zero, parallel and collinear vectors). Position vector of a point, negative of a vector, component of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Scalar (dot) product of vectors, projection of a vector on a line. Vector (cross) product of vectors.
2. Three– Dimensional geometry:
Direction cosines/ratios of a line joining two points. Cartesian and vector equation of a line, coplanar and skew lines, shortest distance between two lines. Cartesian and vector equation of plane. Angle between (i) two lines, (ii) two planes. (iii) a line and a plane. Distance of a point from a plane.
UNIT V. LINEAR PROGRAMMING
Linear Programming:
Introduction, definition of related terminology such as constraints, objective function, optimization, different types of linear programming (L.P.) problems, mathematical formulation of L.P. problems, graphical method of solution for problems in two variables, feasible and infeasible regions, feasible and infeasible solutions, optional feasible solutions (up to three non-trivial constraints).
UNIT VI. PROBABILITY
Probability:
Multiplication theorem on probability. Conditional probability, independent events, total probability, Baye’s theorem, Random variable and its probability distribution, mean and variance of haphazard variable. Repeated independent (Bernoulli) trials and Binomial distribution.
